![]()
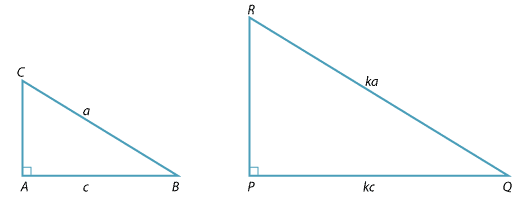
RHS test
The RHS similarity test: If the ratio of the hypotenuse and one side of a right-angled triangle is equal to the ratio of the hypotenuse and one side of another right-angled triangle, then the two triangles are similar.
Example 4
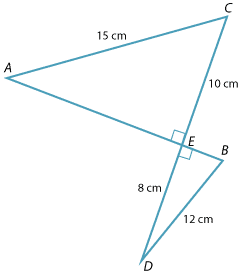
Prove that \(\triangle ACE\) is similar to \(\triangle BDE\).
Solution
In the triangles \(ACE\) and \(BDE\)
\begin{align}\angle AEC = \angle BED &= 90°(given)\\ \dfrac{AC}{CE}&=\dfrac{3}{2}(given)\\ \dfrac{BD}{DE}&=\dfrac{3}{2}(given)\end{align}So \(\triangle ACE\) is similar to \(\triangle BDE\) (RHS similarity test).